Table of Gemstones Hardness, Specific Gravity, R.I.

• How to calculate Specific Gravity - Direct Weighing Method
• How to calculate Specific Gravity - Heavy Liquids

The quantity of matter in a given space is referred to as DENSITY. Expressed scientifically, it is the mass of any substance contained in unit volume. Thus the mass, or quantity, of matter contained in a cube of lead is much greater than that contained in a cube of wood of the same size. The densities of gemstones depend on the closeness with which their atoms are packed and on the weight of those atoms. A Two-carat diamond is much smaller than an amethyst (quartz) of the same weight. To say that a diamond is heavier than an amethyst conveys little information; to arrive at an exact comparison, we must compare the weight of equal volumes of each. Since it would be difficult otherwise to compare volumes accurately, this is accomplished by comparing the weight of each stone with the weight of an equal volume of water. The number of times a stone is heavier than the weight of its own volume of water is called its SPECIFIC GRAVITY (also written S.G. or Sp. Gr.). Thus the specific gravity of gemstone is the ratio of its density to the density of water.

Specific gravity is technically defined as the ratio obtained by dividing, the weight of a body by the weight of an equal volume of distilled water at a temperature of 4°C. (39.2° F.). Water at 4°C. has a maximum density and hence can be used as a standard, but in gem testing it is usually possible to obtain sufficiently accurate results without considering temperature.

The specific gravity of quartz is 2.66, which means that a quartz gem of a given size weight 2 and 66/100 times as much as a volume of water of the same size. Specific gravity is represented by a number that is definite for each species, within certain narrow limits. Hence its determination offers a sure and ready test in the identification of un-mounted fashioned gems without injuring then.

Specific gravity is an important property, not only for the purpose of identification, but because of its effect on the relative size per carat of gems. For example, a one-carat emerald is considerably large than a one-carat diamond, which, in turn, is larger than a one-carat zircon.

Stated another way, the higher the S.G., the smaller the stone per carat, and must give the stones size in millimeters rather than in weight, if he is replacing the original stone with one of another species. Many jewelers become adept at estimating the weight of a diamond by appearance; few, however, are equally proficient in estimating the weight of colored stones. To do so requires a general idea of the relative specific gravities of the various stones. As a further example, a one carat amethyst is much larger in fact, perhaps two-thirds greater in diameter than a zircon of equal weight.

How to Calculate Specific Gravity

There are two principal methods of determining specific gravity.

The Direct Weighing Method

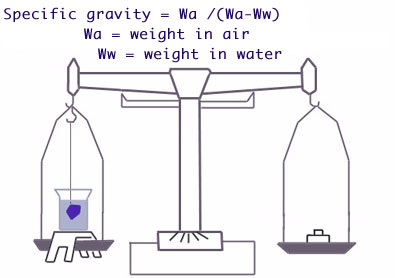
From the definition: specific gravity is equal to the weight of a stone divided by the weight of an equal volume of water. The weight of a stone can be found readily by weighing on an accurate balance. The weight of an equal volume of water can be found by the simple principle discovered by Archimedes, which states that "if a body is totally immersed in water, it loses an amount of weight equal to the weight of the water it displaces. Hence the weight of an equal volume of water is equal to the weight lost by the stone when immersed. Thus:

S.G. = (Weight in Air ) / (Weight in Air - Weight in Water)

In other words, the specific gravity of a stone is the number obtained by dividing its weight in air by its loss of weight when weighed in water. This gives a simple method of finding the S.G. of a cut stone.

In further explanation:

1. Weigh the stone in air; assume this is 4.2 carats.
2. Weigh the stone in water; assume this is 3.0 carats.
3. The difference in the two weighs gives the loss of weight in water: loss of weight: 4.2 - 3.0 = 1.2 carats.
4. S.G. of stone = weight in air divided by loss of weight in water: S.G. = 4.2/1. 2 => 3.5
   (Note that the S.G. is a number that represents a RATIO I not a weight.)

For making S.G. determinations by the direct-weighing methods, a delicate balance, such as a good diamond balance is needed. Weighing the stone in air is simple, but to obtain an accurate weight in water is a slightly more complicated undertaking. The problem is how to weigh the stone in water with a minimum of time and equipment. The balance must be adapted so that the stone can be weighed accurately in air and in water. This is accomplished by using a few simple attachments consisting of two thin wires, a glass beaker and a suitable support. These accessories can be constructed easily or purchased by those who have a diamond balance and who wish to add the necessary equipment.

The small metal support is bridged over one balance pan, so that it does not interfere with the free swing of the balance. The beaker of water is then placed on this stand and one of the thin wires is bent to form a basket at one end to hold the stone. This is suspended from one arm of the balance and immersed in the liquid. The other wire is suspended from the opposite arm of the balance and then clipped or filed off until it balances exactly the wire suspended in the water.

The surface tension of the water acting on the wire at the point where it enters the water causes a damping effect(drag) on the free swing of the balance. This considerably reduces the accuracy normally obtained from the balance. However, a detergent such as "Dreft", "Vel" or "Tide" effectively reduces the surface tension of water, and the pinch or two necessary docs not alter the density of the water sufficiently to require a correction factor. The proper temperature for the distilled water used in the direct weighing method is, as previously mentioned, 4°C, or about 40°F, However, using water at ordinary room temperature of about 70°F, will not materially affect the calculation.

The following example will make the method clear. Given a yellow stone to test:

1. Weight of the stone in air = 12.89 carats.
2. Place the stone in the wire cage, remove all bubbles, and see that it is completely immersed. New weigh the stone carefully in water. It weighs 9.67 carats.
3. Loss of weight in water = 12.89 - 9.67 carats.
4. S.G. = 12.89/3.22 = 4.00
5. Looking up this value in the accompanying table, we see that the stone is probably yellow sapphire (corundum), either natural or synthetic.

It will be noted in the table that normal S.G. values as well as the most generally encountered variations are listed. However, no tolerance is considered for mechanical errors in making S.G. determinations. There is a definite lower limit in the weight of the stone being tested to which diamond-balance determinations can be given any accuracy.

A colored mineral usually varies in specific gravity from one specimen to another, due particularly to slight variations in chemical composition. Therefore, several similar minerals may have the same S.G. because their values overlap, as seen in the table. The values for specific gravity in all mineralogy texts and in some gemology texts are for all varieties of a given mineral species. Such tables may add unnecessarily to the confusion of the gemologist who is using them and who needs to consider only gem qualities of the various species. The figures in the table are for gem materials, and show specific gravity to be one of the more important tests.

To illustrate the effects of errors in weighing, refer again to the example given above. The weight of the stone in air is 12.89 carats and its weight in liquid is 9.67 carats. Suppose a mistake of one point had been made in weighing the stone in liquid. If the weight had been 9.66 instead of the correct 9.67 figure, the difference between 9.66 and 12.89 is 3.23 carats. By dividing 3.23 into 12.89, a specific-gravity determination of 3.99 is made. Therefore, an error of only. 0 1 occurs because of a mistake of one hundredth of a carat in the weight.

A stone that weigh's 1.20 carats in air and 90 points in water would have an S.G. of 4.00. If, however, a mistake is made in the weighing and the weight in water is determined as .89 carats instead of .90, the error will be greater. Dividing 1.20 by .31 gives a resulting S.G. of 3.87; therefore, the error is 0.13. Carrying this example one step further, if a stone weighs .40 carats in air and. 30 carats in water, it has a specific gravity of 4.00. An error in this case of one point, giving a water weight of .29, would result in the determination being 3.63 to 3.64. In other words, an error of more than 0.35 in S.G. would result.

From the above discussion, it can be seen that specific-gravity determinations by the diamond-balance method for stones of less than one-half carat are not accurate unless very careful weightings are made. No such limitation exists when heavy liquids are used instead of the diamond balance.

How to calculate Specific Gravity - Heavy Liquids

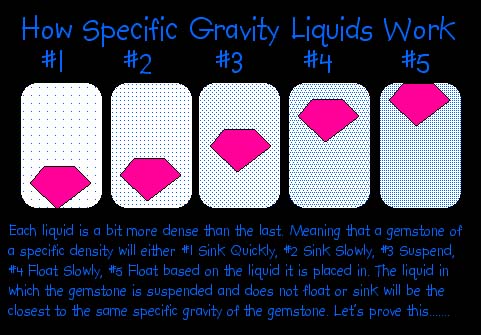
When a solid is placed in a liquid of lower density, it sinks. On the other hand, if its density is lower than that of the liquid, it floats, as does wood in water. If a stone has an S.G. equal to the density of the liquid into which it is dropped, it remains suspended in the liquid. This would have no particular significance if it were not for the availability of a number of liquids with densities up to several times that of water. The advantage of a heavy liquid is that it is so simple and free from the potentiality of arithmetical error. In addition, it provides a very fast method.

Although the obvious findings of the heavy liquids are simply whether the stone has a higher or lower S.G. than the liquid, more information may be gained. As a stone sinks in a liquid, and idea of how much more dense it is than the liquid is furnished by observing how rapidly it sinks. This is affected also by the shape of the stone. For example, a large flat stone will sink more slowly in the flat position than in an upended position. When a stone floats, the percentage above and below the liquid represents the relationship between the two S.G's. In other words, if the stone has 9/10 of its volume beneath the surface, it was an S.G. equal to 9/10 that of the liquid. The exact ratio can be estimated only roughly by eye, but it serves as a guide.

Unfortunately, the heavy-liquid method has a major limitation (in addition to the one that any S.G. method suffers: the restriction to loose stones only), and that is the practical upper limit for safe liquids at 3.32. Above that figure, those that are readily available are either opaque suspensions of finely divided solids in a heavy liquid or Clerici's solution. The latter is poisonous and corrosive, so it is dangerous unless used with caution.

Table of specific gravities of various liquids
Liquid	Specific Gravity
Saturated salt solution	1.15
Carbon tetrachloride	1.59
Bromoform	2.89
Methylene iodide	3.32
Thallium formate and malonate (Clerici's solution)	4.65
Thallium silver nitrate	5.00

A very useful set of heavy liquids consists of three small bottles or beakers, each containing about 25 cc. of a heavy liquid. The first bottle contains methylene iodide (3.32), the second contains bromoform (2.89), and the third bottle contains bromoform diluted with xylene (2.62). By dropping the unknown stone first into one and then into the other Liquid (being careful to wipe the stone thoroughly to avoid contamination of one liquid by another), it is possible to place it into one of the following four broad groups:

1. Floats in 2.62 Liquid.
2. Sinks in 2.62 liquid and floats in 2.89 liquid.
3. Sinks in 2.89 Liquid and floats in 3.2 liquid.
4. Sinks in 3.32 liquid.

If desired, additional liquids having intermediate S.G.'s may be prepared by diluting pure methylene iodide or bromoform with different amounts of xylene and using the following gems as indicators to calibrate the liquids; moonstone (2.56), quartz (2.66), aquamarine (2.72), nephrite (2.95), tourmaline (3.06), kunzite (3.18). The methylene iodide or bromoform is diluted until one of these gems remains suspended in the liquid. However, since xylene evaporate more rapidly than either of the other chemicals, the bottles should be kept tightly closed if the liquids are to remain constant. In addition, the indicators should be left in the bottles at all times so that an immediate visual check of the value of the liquids can be made.

Because of the low cost and the rapidity with which reasonably accurate determinations can be made, a set of heavy liquids should be one of the first acquisitions for any gem-testing laboratory. Of course, for a wider range of S.G.'s, the direct weighing method with the diamond balance is necessary.